In questo scritto si vuole approfondire teoricamente il significato di distorsione armonica e di rumore, definendo i principali indici utilizzati per la loro valutazione. La comprensione presuppone la conoscenza di alcune nozioni di analisi matematica.

Serie di Fourier

Una generico segnale periodico f(t), che si ripete nel tempo con periodo T, frequenza f=1/T e pulsazione w=2*pigreco*f, può essere espresso come somma di segnali sinusoidali di frequenza f (fondamentale) e multipli di f (armoniche), l’espressione analitica che rappresenta quanto detto è la serie di Fourier:

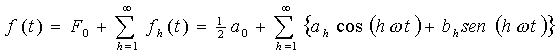
con a_h e b_h calcolati nel modo seguente:


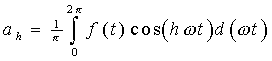
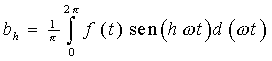
in cui il termine

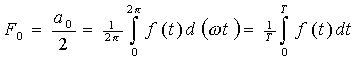
non è altro che il valore medio del segnale considerato.

Il generico termine

è una singola componente di frequenza, f₁ è la componente fondamentale ed f_h (per h>1) è detta armonica (h-1)esima di f(t).
Il valore efficace della componente f_h(t) è pari a:

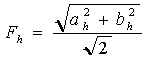
Il valore efficace (rms) del segnale f(t) può essere espresso in termini del valore rms delle singole componenti della sua serie di Fourier nel modo seguente:

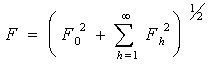
La serie di Fourier può essere espressa sotto forme diverse utilizzando soli termini esponenziali o cosinusoidali, nell’ultimo caso abbiamo:

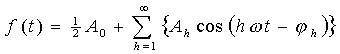
ponendo:

con A₀=a₀ e

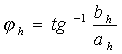
con l’ovvia corrispondenza:

La successione di numeri A₀ /2, A₁ , …, A_h prende il nome di spettro di ampiezza della funzione f(t), con A₀ /2 detta componente costante, la successione fi₁ , fi₂ , …, fi_h di spettro di fase e il termine

è equivalente all’espressione di f_h vista precedentemente. Ognuno di questi non è altro che una sinusoide di frequenza f=h*w/2pigreco, che nel dominio della frequenza corrisponde ad un impulso centrato a frequenza f.

Distorsione armonica

Consideriamo un segnale senza alcuna armonica, ovvero una sinusoide perfetta che quindi ha solo la componente a frequenza fondamentale, attraversando un certo circuito questo introduce certamente una distorsione, ovvero modifica il segnale rispetto a quello originario. Ciò comporta in uscita la presenza di un segnale che non è più una sinusoide pura, vi è allora un certo numero di armoniche che prima non esistevano. La loro misura indica l’entità della distorsione introdotta dal circuito o da un sistema in generale.
Tornando alle parte analitica separando il primo termine della sommatoria della serie di Fourier possiamo esprimere il segnale in questione come:

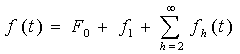
sia:

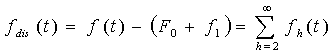
la componente distorsiva presente in f(t),

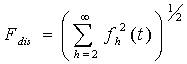
il suo valore rms ed F₁ o F il valore rms della fondamentale (h=1).

Si definiscono i seguenti indici:
Distorsione armonica individuale IHD (Individual Harmonic Distortion)

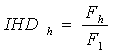
calcolato in riferimento alla singola armonica di frequenza h volte la fondamentale.
Distorsione armonica totale THD (Total Harmonic Distortion)

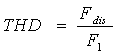
in riferimento a tutte le armoniche esistenti.
Questi valori vengono solitamente espressi in percentuale moltiplicando per 100 il valore ottenuto dalle precedenti espressioni:
IHD%=IHD*100     THD%=THD*100

Alcune volte il sistema introduce oltre alle armoniche anche componenti a frequenza diversa da multipli della fondamentale, queste componenti prendono il nome di spurie.

Rumore

Il rumore è quella porzione di segnale indesiderata e distruttiva ai fini del trasporto delle informazioni, che va ad aggiungersi al segnale utile. La sua presenza è dovuta a disturbi che possono generarsi all’interno del sistema o che provengono dall’esterno dello stesso, la natura del rumore è quindi molto varia come ampiezza e spettro e a volte non è prevedibile.
La quantità di rumore presente rispetto al segnale utile si indica con i seguenti indici:
Rapporto segnale rumore S/N o SNR (Signal to Noise Ratio)


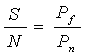
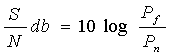
con P_f potenza del segnale utile e P_n potenza di rumore.
Tenendo anche conto della distorsione armonica:
Rapporto segnale rumore e distorsione SINAD (Signal to Noise And Distortion)


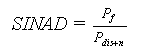
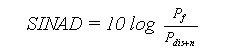
Nelle espressioni viste compaiono delle potenze medie P, in realtà trattandosi di rapporti possiamo fare riferimento a potenze calcolate su carichi unitari, il loro valore è quindi uguale al quadrato del valore efficace ottenendo:



avendo indicato con N il valore efficace del rumore.

---

Autore: Gianfranco IZ8EWD
Data di pubblicazione: 12/2005

---

Questa opera è distribuita con:
licenza Creative Commons Attribuzione - Non commerciale - Condividi allo stesso modo 3.0 Italia.

Si declina ogni responsabilità per eventuali errori ed omissioni e gli eventuali danni che ne dovessero conseguire. Per ulteriori informazioni consultare le note legali.